高中“方程的根与函数的零点”(第一节课)设定的教学目标如下:
①通过对二次函数图象的描绘,了解函数零点的概念,渗透由具体到抽象思想.领会函数
零点与相应方程实数根之间的关系.
②理解提出零点概念的作用,沟通函数与方程的关系。
③通过对现实问题的分析,体会用函数系统的角度去思考方程的思想,使学生理解动与静
的辩证关系。掌握函数零点存在性的判断。
完成下列任务:
根据教学目标,设计一个问题引入,并说明设计意图;

设计意图:以学生熟悉二次函数图象和二次方程为平台,观察方程和函数形式上的联系.从而得到方程实
数根与函数图象之间的关系。理解零点是连接函数与方程的结点。
根据教学目标①,设计问题链(至少包含三个问题),并说明设计意图:

设计意图:以学生熟悉二次函数图象和二次方程为平台,观察方程和函数形式上的联系.从而得到方程实
数根与函数图象之间的关系。理解零点是连接函数与方程的结点。
根据教学目标③,给出至少一个实例和三个问题,并说明设计意图:
实例:如果把函数比作一部电影,那么函数的零点就像是电影的一个瞬间,一个镜头。有时我们会忽略
一些镜头,但是我们仍然能推测出被忽略的片断。现在我有两组镜头(图略),哪一组能说明他的行程一定曾渡
过河?
设计意图:从现实生活中提出的问题,让学生体会动与静的关系,系统与局部的关系。
问题①:将河流抽象成x轴,将前后的两个位置视为a、b两点。请问当a、b与x轴是怎样的位置关系时,ab
间的一段连续不断的函数图象与x轴一定会有交点?

设计意图:将现实生活中的问题抽象成数学模型,进行合情推理,将原来学生只认为静态的函数图象,理解
为一种动态的过程。
问题②a、b与x轴的位置关系,如何用数学符号(式子)来表示?
设计意图:由原来的图象语言转化为数学语言。培养学生的观察能力和提取有效信息的能力。体验语育转
化的过程。
问题③:满足条件的函数图象与x轴的交点一定在(a,b)内吗?即函数的零点一定在(a,b)内吗?
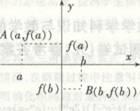
设计意图:让学生体验从现实生活中抽象成数学模型时,需要一定修正。加强学生对函数动态的感受,对函
数的定义有进一步的理解。
确定本节课的教学重点:
教学重点:了解函数零点的概念,体会方程的根与函数零点之间的联系,掌握函数零点存在性的判断。
作为高中阶段的基础内容,其难点是什么?
教学难点:准确认识零点的概念,在合情推理中让学生体会到判定定理的充分非必要性,能利用适当的
方法判断零点的存在或确定零点。
本节课的教学内容对后续哪些内容的学习有直接影响?
本节课是在学生学习了《基本初等函数(i)》的基础上,学习函数与方程的第一课时,本节课中通过对
二次函数图象的绘制、分析,得到零点的概念,从而进一步探索函数零点存在性的判定,这些活动就是想让学生
在了解初等函数的基础上,利用计算机描绘函数的图象,通过对函数与方程的探究,对函数有进一步的认识,解
决方程根的存在性问题,为下一节《用二分法求方程的近似解》做准备。

微信扫一扫手机做题
